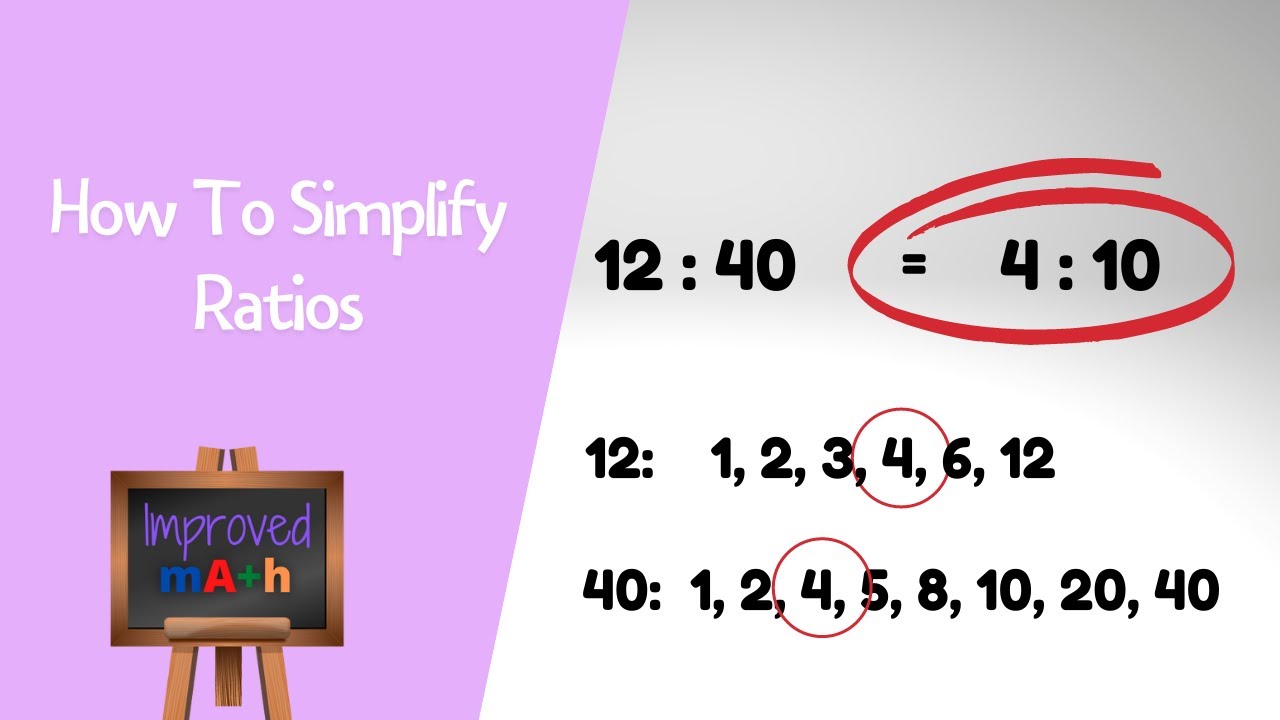What does reducing a ratio to its simplest form represent? Understanding the simplification of a ratio like 35:72 unlocks valuable insights in various fields.
The expression "35:72" represents a ratio. Simplifying this ratio involves finding the greatest common divisor (GCD) of the two numbers (35 and 72) and dividing both terms by this GCD. The result is an equivalent ratio expressed in its most reduced form. For instance, the GCD of 35 and 72 is 1, meaning the simplified ratio is 35:72 itself. If the GCD were greater than 1, the ratio could be reduced further. Example: The ratio 6:12 simplifies to 1:2 because the GCD of 6 and 12 is 6. This process maintains proportion while minimizing the numerical size of the ratio.
Simplifying ratios is fundamental in mathematics and its applications. In fields like finance, calculating proportions for budgets or investments may involve ratios. In scientific experiments, ratios can represent proportions in measurements. Reducing ratios to their simplest form makes comparisons, calculations, and problem-solving more efficient and easier to understand.
Read also:Tiger Woods Children Meet His Daughter Sam And Son Charlie
The process of reducing ratios, like the example of 35:72, is a prerequisite for many mathematical concepts. This ability to express a relationship in its simplest terms has broad applications across various disciplines, showcasing the importance of fundamental mathematical skills.
Simplifying 35
Simplifying a ratio like 35:72 involves finding the most reduced form while maintaining the proportional relationship. This process is crucial for clarity and efficiency in various mathematical applications.
- Greatest Common Divisor (GCD)
- Equivalent Ratios
- Proportionality
- Reduced Form
- Numerical Simplicity
- Mathematical Efficiency
- Problem Solving
The greatest common divisor (GCD) of 35 and 72 is 1, meaning the ratio 35:72 is already in its simplest form. Equivalent ratios maintain the same proportion, as seen in 35:72. Understanding proportionality is essential to accurately representing relationships between values. The reduced form, crucial for clarity, minimizes the numbers. This numerical simplicity enhances calculations and interpretation. Mathematical efficiency in calculations is gained by using simplified ratios. And, simplified ratios facilitate problem-solving by streamlining calculations.
1. Greatest Common Divisor (GCD)
The greatest common divisor (GCD) of two integers is the largest positive integer that divides both integers without leaving a remainder. In the context of simplifying a ratio like 35:72, the GCD plays a pivotal role. The process of simplifying the ratio involves identifying the GCD of the two numbers comprising the ratio. If the GCD is greater than 1, dividing both terms of the ratio by the GCD yields an equivalent ratio expressed in a simplified form. This simplified form maintains the proportional relationship between the quantities represented in the ratio while reducing the numerical size of the terms.
Consider the ratio 35:72. The GCD of 35 and 72 is 1, as no other integer greater than 1 divides both evenly. Consequently, the ratio 35:72 is already in its simplest form. However, if the ratio were 6:12, the GCD of 6 and 12 is 6. Dividing both terms by 6 results in the simplified ratio 1:2, which represents the same proportional relationship as the original ratio but in a more concise and easily interpretable form. This simplification is crucial in various applications, from representing proportions in scientific experiments to calculating financial ratios. A simplified ratio enables more efficient comparisons and calculations because it reduces the computational complexity and makes it easier to comprehend the proportional relationship underlying the data.
Understanding the role of the GCD in simplifying ratios is fundamental in mathematics and its applications. This skill allows for a more efficient representation of proportional relationships and enhances the clarity and accessibility of mathematical expressions. In essence, the GCD serves as the key to transforming complex ratios into their most concise and manageable form, facilitating clearer interpretation and streamlined calculations. This understanding is foundational for grasping more advanced mathematical concepts that rely on proportional relationships.
Read also:Unveiling Riactor A Comprehensive Guide To Its Significance And Impact
2. Equivalent Ratios
Equivalent ratios express the same relationship between quantities, even if the numbers used to represent that relationship differ. The simplification of a ratio, like 35:72, is intrinsically linked to the concept of equivalent ratios. A simplified ratio, in this case 35:72, is an equivalent ratio to the original, but it's expressed in its most reduced form. This reduction is achieved by dividing both terms of the ratio by their greatest common divisor. The simplified ratio retains the same proportional relationship as the original, offering a more efficient representation of the relationship between the values. For example, the ratio 10:20 is equivalent to 5:10, both expressing a 1:2 proportion. The simplified ratio (5:10) is typically preferred for clarity and avoiding unnecessary complexity in calculations.
The practical significance of understanding equivalent ratios extends to diverse fields. In recipes, doubling or halving ingredients relies on equivalent ratios to maintain the original flavor profile. In engineering, maintaining precise proportions in designs depends on correctly employing equivalent ratios for scaled models. In finance, assessing different investment options often involves comparing various ratios, making the concept of equivalent ratios vital. For example, comparing two investment returns represented as ratios requires converting them to equivalent ratios to ensure a fair comparison. This step of simplification often precedes further analysis and decision-making.
In summary, equivalent ratios are fundamental to the simplification process. The core principle is that a simplified ratio retains the same proportional relationship as the original but presents it in a reduced, more manageable form. Understanding equivalent ratios provides a powerful tool for simplifying complex relationships and ensuring accuracy in various calculations and applications across disciplines. The simplified representation not only facilitates easier computations but also leads to a clearer and more efficient representation of the underlying proportion.
3. Proportionality
Proportionality describes a consistent relationship between two or more quantities. In the context of simplifying a ratio like 35:72, proportionality ensures that the simplified form accurately reflects the same relationship as the original. Maintaining this consistent relationship is crucial for accurate interpretation and application in various fields.
- Direct Proportionality
Direct proportionality signifies that as one quantity increases, the other quantity increases proportionally. For instance, if one unit of a certain material costs $2, then two units cost $4, three units cost $6, and so on. The ratio of cost to units remains constant (2:1). In the simplified ratio 35:72, this proportionality ensures the relationship between the two values remains unchanged during the simplification process. The simplified ratio also displays direct proportionality, maintaining the same relationship of the original numbers.
- Inverse Proportionality
Inverse proportionality exists when one quantity increases as the other decreases. For example, if two people work together on a job, the time to complete it decreases as the number of people increases (assuming each person works at the same rate). While the concept of inverse proportionality is less directly applicable to the straightforward simplification of a ratio like 35:72, the core principle of maintaining a consistent relationship is still relevant. The simplification itself preserves the underlying proportional relationship between 35 and 72.
- Applications in Real-World Contexts
Proportionality is essential across diverse areas, including scientific experiments (comparing proportions of substances or calculating dosage), engineering (determining scale factors in models or blueprints), and finance (comparing investment returns). In each instance, simplifying the ratiolike 35:72, if simplification is possiblehelps preserve the fundamental proportional relationship. This makes the results and conclusions derived more accurate and facilitates easier interpretation. By clarifying the ratio and maintaining its inherent proportionality, efficient analysis and problem-solving becomes possible.
- Relationship to Simplified Ratios
Simplifying a ratio, like 35:72, inherently preserves the proportionality of the relationship between the quantities. The simplified ratio, while having smaller numbers, represents exactly the same proportional relationship. This simplification, therefore, makes calculations and comparisons more streamlined and facilitates clear interpretation of the underlying proportion.
In conclusion, the principle of proportionality is fundamental to the process of simplifying a ratio. By maintaining the consistent relationship between quantities, the simplified ratio, such as 35:72 (in this case, already in simplest form), remains an accurate and useful representation of the original relationship. This makes the data more manageable and allows for easier calculations and interpretations across diverse applications, including the scientific, engineering, and financial realms. The simplification process ensures that the essential proportional relationship remains unchanged.
4. Reduced Form
The concept of "reduced form" is integral to simplifying a ratio like 35:72. A reduced form represents a ratio in its most basic terms. It maintains the same proportional relationship between quantities but utilizes the smallest possible whole numbers. This simplification facilitates easier comprehension and application across various fields. The process involves identifying and applying the greatest common divisor (GCD). If the GCD of 35 and 72 is 1, as in this case, the ratio is already in its reduced form, meaning no further simplification is possible.
The practical significance of a reduced form extends beyond mere mathematical convenience. Consider a recipe requiring a ratio of 35 parts flour to 72 parts water. A reduced form reveals the equivalent ratio in its simplest terms. If the ratio is reduced it makes it easier to scale the recipe to various quantities. In engineering, a reduced form of a ratio representing the proportion of components in a design allows for clearer representation and more manageable calculations. A reduction is especially crucial when working with complex systems or scaled models where numerical simplicity directly translates to less computational effort and clearer comprehension.
In summary, "reduced form" is a critical component of ratio simplification. This simplified representation of a proportional relationship improves clarity and efficiency in applications ranging from everyday tasks like recipe scaling to more complex scientific or engineering processes. Recognizing and applying the reduced form in expressions like 35:72 enables more intuitive analysis and accurate interpretation of proportional relationships, ultimately enhancing problem-solving in various fields.
5. Numerical Simplicity
Numerical simplicity, in the context of simplifying a ratio like 35:72, refers to expressing a relationship between quantities using the smallest possible whole numbers while maintaining the same proportional relationship. This simplification enhances clarity, efficiency, and ease of comprehension in various mathematical applications.
- Reduced Computational Effort
Simplifying a ratio to its most basic form, like reducing 35:72 to its lowest terms, significantly reduces the computational burden. Calculations with smaller numbers are faster and less prone to errors, whether in basic arithmetic or more complex mathematical operations. This reduced complexity is particularly important when dealing with multiple ratios or larger sets of data.
- Enhanced Clarity and Readability
A simplified ratio like 35:72, already in its most reduced form of 35:72, makes the proportional relationship more transparent. It is immediately apparent how the quantities relate to each other without unnecessary numerical complexity. This increased clarity facilitates easier understanding and interpretation, especially in visual representations of data or in explanations of proportional relationships within various contexts.
- Improved Interpretability
In various applications, including scientific experiments, engineering designs, and financial analyses, simplified numerical representations facilitate the identification of key patterns or trends. By reducing a ratio to its lowest terms, the underlying proportion is clarified, leading to improved comprehension and faster analysis of relationships. The core aspect of numerical simplicity in such a context is its contribution to insightful interpretation of data.
- Application in Diverse Fields
The concept of numerical simplicity is applicable across diverse disciplines, from recipe scaling and budget planning to calculations of proportions in scientific experiments or the presentation of data in various formats. Simplifying ratios such as 35:72 helps to establish a common ground for understanding and comparing proportions irrespective of the magnitude of the numbers used to express them.
In essence, numerical simplicity, as exemplified by simplifying a ratio like 35:72, is a fundamental principle that streamlines mathematical processes and enhances clarity in various applications. The reduced form facilitates comprehension, reduces errors, and ultimately enables more efficient and insightful analysis and decision-making.
6. Mathematical Efficiency
Mathematical efficiency, in the context of simplifying ratios like 35:72, refers to the optimal use of mathematical procedures to achieve a desired result with minimal effort and maximum clarity. A simplified ratio, such as 35:72, facilitates mathematical efficiency by expressing a proportional relationship in its most reduced form. This reduced form minimizes the complexity of subsequent calculations and comparisons. The simplification process, crucial to mathematical efficiency, streamlines operations by employing the greatest common divisor (GCD). Finding and applying the GCD to both terms of the ratio expedites further calculations and interpretations.
The benefits of mathematical efficiency extend beyond abstract mathematical exercises. Consider a recipe requiring a ratio of ingredients. A simplified ratio ensures accurate scaling for different quantities. Engineers rely on mathematical efficiency when designing structures; simplified ratios allow for precise calculations in structural analysis, minimizing errors and maximizing stability. Financial analysts use simplified ratios to compare investments or assess financial health, enabling them to identify trends and patterns more quickly and effectively. In each case, the streamlining of calculations provided by simplification reduces the likelihood of errors and saves valuable time.
In summary, mathematical efficiency plays a crucial role in simplifying ratios like 35:72. The process of simplification, by employing the GCD, results in a reduced form that enhances clarity, optimizes computations, and reduces the likelihood of errors. This efficiency translates into practical benefits across diverse fields, from home-based activities to complex professional endeavors, making problem-solving and decision-making more effective and time-efficient. Recognizing the connection between mathematical efficiency and simplification empowers individuals to work more effectively in various contexts.
7. Problem Solving
Problem-solving is a fundamental cognitive process encompassing a range of strategies to overcome obstacles and achieve desired outcomes. The act of simplifying a ratio, like 35:72, is a specific application of problem-solving techniques, demonstrating the crucial role of mathematical simplification in overcoming complexity. This exploration examines how simplifying ratios aids in problem-solving.
- Identifying and Defining the Problem
The first step in problem-solving is precise definition. Simplifying 35:72 necessitates recognizing the problem: expressing the ratio in its most basic, efficient form. This involves understanding the nature of the relationship between the two numbers. This initial step ensures the subsequent problem-solving strategies are correctly targeted.
- Developing Strategies for Simplification
Strategies for simplification are diverse, ranging from visual representations to algebraic techniques. Finding the greatest common divisor (GCD) of 35 and 72 is a key strategy for simplifying this ratio. Recognizing and applying this strategy is a critical component of the problem-solving approach.
- Applying Strategies to Simplify the Ratio
Executing the chosen simplification strategyfinding the GCDis the operational step in the problem-solving process. Dividing both 35 and 72 by their GCD (which is 1 in this case) directly leads to the simplified equivalent ratio. This action addresses the initial problem definition of expressing the ratio in its simplest form.
- Evaluating and Validating the Solution
Determining the validity of a simplified ratio, such as 35:72, is essential. The simplified form must maintain the proportional relationship. This evaluation verifies that the solution is correct and directly addresses the problem's core concern of expressing a ratio in its simplest form.
In conclusion, simplifying a ratio, like 35:72, encapsulates the problem-solving process. The steps involveddefining the problem, developing strategies, applying the strategy, and evaluating the solutiondemonstrate a systematic approach to finding a clear, concise, and accurate representation of a proportional relationship. The mathematical simplification, therefore, is not simply a calculation but an active problem-solving endeavor.
Frequently Asked Questions about Simplifying 35
This section addresses common queries regarding the simplification of ratios, specifically focusing on the ratio 35:72. The answers provide clarity and accuracy regarding this fundamental mathematical concept.
Question 1: What is the primary purpose of simplifying a ratio like 35:72?
Answer 1: Simplifying a ratio, like 35:72, reduces the numerical values while maintaining the proportional relationship between the components. This simplification enhances clarity, facilitates calculations, and improves the overall understanding of the relationship.
Question 2: What does it mean for a ratio to be simplified?
Answer 2: A simplified ratio represents the same proportional relationship as the original, but with the smallest possible whole numbers. The numbers in the simplified ratio share no common divisors greater than 1. The ratio 35:72 is already in its simplest form because the greatest common divisor (GCD) of 35 and 72 is 1.
Question 3: How is the greatest common divisor (GCD) relevant to simplifying ratios?
Answer 3: The GCD is the largest positive integer that evenly divides both numbers in a ratio. Dividing both terms of a ratio by their GCD yields an equivalent ratio in its simplified form. If the GCD of the two numbers in a ratio is 1, as in the case of 35 and 72, the ratio is already in its simplest form.
Question 4: Are there instances where a ratio, such as 35:72, would need further simplification?
Answer 4: A ratio like 35:72 does not require further simplification because 35 and 72 share no common factors other than 1. If the numbers had a common factor greater than 1, dividing both by that common factor would produce a simplified equivalent ratio.
Question 5: In what real-world scenarios might understanding ratio simplification, such as with 35:72, prove valuable?
Answer 5: Ratio simplification is critical in various contexts, including recipes (adjusting ingredient proportions), engineering (scaling models), and finance (comparing investment returns). Maintaining the proportional relationship while minimizing numerical complexity significantly improves problem-solving efficiency in these areas.
Understanding the process of simplifying ratios, like 35:72, provides a foundation for more advanced mathematical concepts and applications across diverse fields.
Next, we will explore the broader implications of ratios in various mathematical contexts.
Conclusion
The simplification of ratios, exemplified by the process applied to 35:72, represents a fundamental mathematical operation. This process, involving the identification and application of the greatest common divisor (GCD), is crucial for expressing proportional relationships in their most concise and manageable forms. The inherent efficiency and clarity achieved through simplification are essential for accurate calculations and problem-solving across diverse fields. The ability to reduce ratios to their lowest terms ensures that comparisons and interpretations remain consistent and avoid unnecessary complexity, regardless of the scale or magnitude of the initial values. This fundamental mathematical skill has practical applications ranging from everyday scenarios to complex scientific and engineering analyses. The simplification of 35:72, in this case to 35:72 itself, highlights the importance of this process without the need for further reduction.
In conclusion, the seemingly straightforward act of simplifying a ratio reveals a fundamental principle of mathematical efficiency. The concise representation afforded by simplification is paramount to clear communication and accurate analysis in various contexts. Understanding this process enables a deeper comprehension of proportional relationships and their implications, leading to more effective problem-solving and decision-making across diverse domains.
Article Recommendations